Recent searches
Search options
#geometry
15 posts12 participants0 posts today
Un pavage de Truchet modifiable en cliquant sur les triangles d'une zone bien précise.
https://www.geogebra.org/m/pngnrsgh
GIF
Patrons de pyramides "coupées" par un plan.
GIF
Patrons de pyramide à base régulières.
Un alternative au patrons générés par #geogebra.
GIF
2 knots: trefoil and pentafoil composed of rhombicosidodecahedra that can represent points as well #math #topology #geometry #geometrictopology #knots #knottheory
GIF
GIF
Continued thread
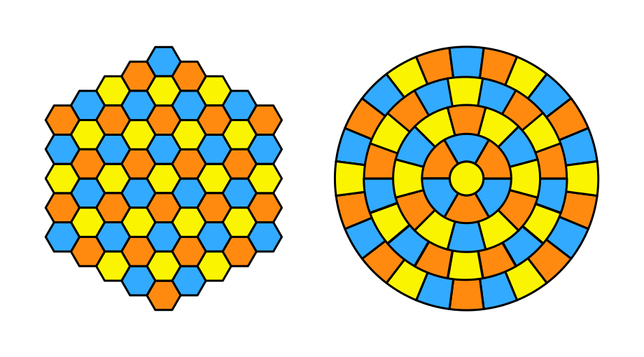
These two art pieces are based on the deformation of a hexagonal tiling into a topologically equivalent "tiling" composed of parts of concentric circles, all parts having the same area (third image). Selecting one hexagon as the center, we transform it into a circle of radius 1. Next concentric circle will hold the 6 adjacent tiles as sectors of rings. And so on, the circle of level n will have radius sqrt(1+3·n·(n+1)) (difference of radius when n tends to infinity approaches sqrt(3)). This map can be coloured with three colours, like the hexagonal tiling. For the artwork, suppose each sector of ring is in fact a sector of a circle hidden by inner pieces. Then choose a colour and delete all pieces not of this colour. Two distinct set of sectors can be produced, one choosing the central colour, one choosing another colour. Finally recolour the pieces according to its size.
#MathArt #Art #Mathematics #geometry #tiling
Graphic design of a Stewart star dodecahedral polytoroid and 3D print: design components: cubes, J92s, J5s, decagonal pyramids. #3dprintedmath #3dprinting #stem #steam #geometry #polyhedra #math #mathart #art
Continued thread
Continuing with fractals related to squares and silver ratio diminution, a new creature of the fractal sea, along with the underlying squares version.
#MathArt #art #SilverRatio #geometry #Mathematics #fractal
Peering down the spiral #staircase in JC Contemporary last week. 
I was pleasantly surprised to find it was open because of Central Galleries Day (normally it’s closed on Mondays). Tai Kwun, #HongKong.
#TilingTuesday 2d cross-section of an 8d point arrangement in ðe hypercubic honeycomb, wiθ 1 point at ðe center of each non-vertex facet & a sphere 10^-5 times ðe radius at ðe center of each 8-cube 𓅱
Celebrate diversity!
#transdayofvisibility #MathArt #geometry
Rhombicosidodecahedron
Face to face tiling 240 equilateral polyhedra.
GIF
Another subfractal with diminution related to the silver ratio.
#MathArt #SilverRatio #geometry #Mathematics #fractal
"Henry Dudeney [...] asked his readers to dissect an equilateral triangle into the smallest number of pieces that could be rearranged into a square.
[...]
Kamata and two other mathematicians have finally proved that a solution with fewer [than four] pieces is impossible. Their result was posted to the server arXiv.org in a December 2024 preprint entitled “Dudeney’s Dissection Is Optimal.”"
On arXiv [ https://arxiv.org/abs/2412.03865 ]
Scientific American · Mathematicians Find Proof to 122-Year-Old Triangle-to-Square Puzzle