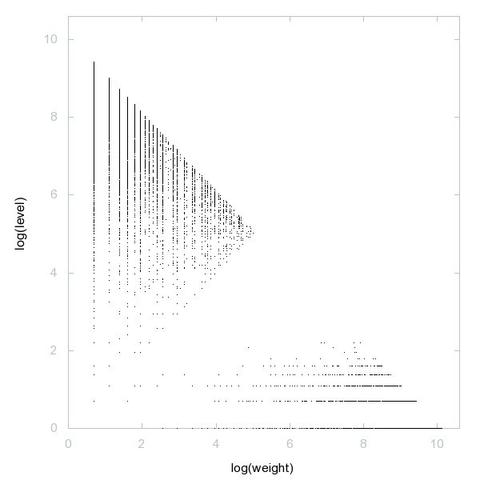
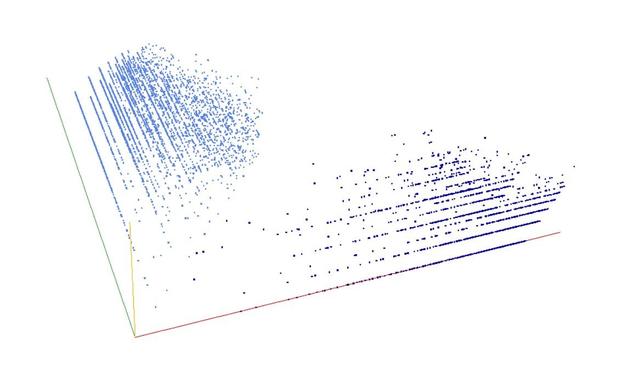
Arithmetic progressions - almost periodicity (A digitisation of the Kelley-Meka bound on Roth numbers in Lean). ~ Thomas Bloom, Yaël Dillies. https://yaeldillies.github.io/LeanAPAP/ #ITP #LeanProver #Math
Recent searches
Search options
#math
Toric varieties in Lean (Formalisation of toric varieties in Lean 4). ~ Yaël Dillies, Paul Lezeau, Patrick Luo, Michał Mrugała, Justus Springer, Andrew Yang. https://yaeldillies.github.io/Toric/ #ITP #LeanProver #Math
Chandra-Furst-Lipton (A digitisation of the number on the forehead model in Lean). ~ Yaël Dillies. https://yaeldillies.github.io/ChandraFurstLipton/ #ITP #LeanProver #Math
Formalizing value distribution theory in Lean. ~ Stefan Kebekus. https://github.com/kebekus/ProjectVD #ITP #LeanProver #Math
Prime number theorem and more in Lean. ~ Alex Kontorovich. https://alexkontorovich.github.io/PrimeNumberTheoremAnd/web/ #ITP #LeanProver #Math
Central limit theorem in Lean. ~ Rémy Degenne. https://remydegenne.github.io/CLT/blueprint #ITP #LeanProver #Math
Lecture notes for an introductory course in group theory. ~ Ben Selfridge. https://github.com/benjaminselfridge/group-theory-course/tree/main #ITP #LeanProver #Math
Verified program extraction in number theory: The fundamental theorem of arithmetic and relatives. ~ Franziskus Wiesnet. https://arxiv.org/abs/2504.03460 #ITP #Minlog #Haskell #FunctionalProgramming #Math

One day, one decomposition
A230044: Nonnegative numbers k such that k plus a perfect square is a triangular number
3D graph, threejs - webGL https://decompwlj.com/3Dgraph/A230044.html
2D graph, first 500 terms https://decompwlj.com/2Dgraph500terms/A230044.html
@paninid fast forward to the present and scientists who barely study #philosophy label #metaphysics as #pseudoscience (forgetting what #PhD means), torment #logic for the benefit of "elegant" #math equations (e.g. antimatter, dark #matter), and design #AI #systems that weaponize #ethics as justification for #information #censorship (#ChatGPT "knows" but refuses to answer how to a hot wire a car or commit murder while claiming no #opinion, ignorant that words and actions are different)
This is where a new variant of the criterion can be applied, this time with the prime number 3.
Indeed, modulo 3, one has f(T)=T^4+2T^2+1=(T^2+1)^2.
So we are almost as in the initial criterion, but the polynomial T is not T^2+1.
The first thing that makes this criterion apply is that T^2+1 is irreducible modulo 3. In this case, this is because -1 is not a square mod 3.
The criterion also requires of variant of the condition on the derivative — it holds because the polynomial is not zero modulo (T^2+1, 9). Here, one has
T^4-10T^2+1=(T^2+1)^2-12T^2 = (T^2+1)^2-12(T^2+1)+12 is equal to 3 modulo (T^2+1, 9).
And so we have an Eisenstein-type proof that the polynomial T^4-10T^2+1 is irreducible over the integers. CQFD.
#math
(#math thread)
Recently, in the Zulip server for Lean users, somebody went with something that looked like homework, but managed to sting me a little bit.
It was about irreducibility of polynomials with integer coefficients. Specifically, the guy wanted a proof that the polynomial T^4-10 T^2+1 is irreducible, claiming that the Eisenstein criterion was not good at it.
What was to proven (this is what *irreducible* means) is that it is impossible to write that polynomial as the product of two polynomials with integer coefficients, except by writing
T^4-10 T^2+1 as (1)·(T^4-10 T^2+1) or as (-1)·(-T^4+10 T^2-1).
"The formula used by the Trump administration to levy reciprocal tariffs contains a serious math error that over-inflates the impact by about a factor of four, economists at the American Enterprise Institute said."

Demostraciones con Lean4 y con Isabelle/HOL de "s ⊆ f⁻¹(f(s))". https://jaalonso.github.io/calculemus/posts/2021/06/07-imagen_inversa_de_la_imagen/ #LeanProver #IsabelleHOL #Math #Calculemus

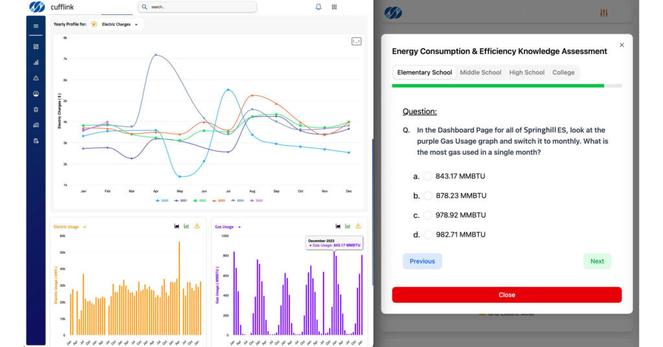
Students Engage with Their Schools’ Energy Data in Cufflink Quizzes https://www.byteseu.com/896168/ #Computer&Electronics #DataAnalytics #EDUCATION #Energy #engineering #Math) #MountainVectorEnergy #NewProducts&Services #STEM(Science #TECH
https://www.europesays.com/1972133/ Scientists Are Mapping the Boundaries of What Is Knowable and Unknowable #america #math #physics #QuantaMagazine #science #technology #UnitedStates #UnitedStatesOfAmerica #US #USA

Patrons de pyramides "coupées" par un plan.
Patrons de pyramide à base régulières.
Un alternative au patrons générés par #geogebra.